
MORE EXAMPLES
These additional examples are classified by increasing complexity.
Strategies for success are described.
- Scratch examples taken from the Endeavour software list of test files (Al2O3, aragonite, CaF2, calcite, forsterite), in the context of the ESPOIR-Endeavour challenge (see the SDPD Mailing List).
- Other more complex scratch examples (Li3RuO4, CuVO3, TeI, PbSO4, Ba2CdP3O10(OH), [Co(NH3)5CO3]NO3.H2O, cimetidine, C60).
- Simple molecule location examples (pyrene, RKSA1), with or without torsion angles.
- Complex examples including several objects (1-methylfluorene, cimetidine).
Copyright © 1999, 2000 - Armel Le Bail
This example will illustrate simply how guessed constraints on occupation numbers and special positions allow to obtain more surely the solution, provided the constraints are true...
A first test is already in the ESPOIR 3.00 package (al2o3.dat) with ns=1, testing the models on the pattern regenerated from the "|Fobs|", and with nob=1 and nobt=1, thus working in pure scratch mode, with ntest=10 (10 independent runs).
Now the second test on Al2O3 will work with ns=0 (the fit is directly on the "|Fobs|") (al2o3F.zip) :
Al2O3 R-3c 4.764 4.764 13.009 90.0 90.0 120.0 R -3 C 1.54056 4 2 2 1 0 1 <-- ns=0, the U,V,W,step line is removed Al+3O-2 1 3.0 1.6 2.2 6. 6. 2. 1.0 0.002 5000 20000 20000 5000 0.2 2 10 1 10 1 1 1.0 1 0 <--- nocc=1, the occupation numbers are read below 2. 3. the occupation numbers could be 0.3333 0.5 as wellThis is at least 5 times faster than the previous run on the regenerated pattern. The results are similar because there is not much overlapping problems in that very simple case. The best result is :
Test number : 10 8-Apr-2000 Hour: 14 Min: 30 Sec: 16 ISEED = 661750968 64 moves acc. 18000 gen. 14162 tested; R=0.005 0 perm. acc. 1999 tested 2 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Al1 0.99477 0.00457 0.85207 2.000 O1 0.65924 0.02364 0.58394 3.000 8-Apr-2000 Hour: 14 Min: 30 Sec: 35 Final RF factor = 4.9909521E-03The third test for Al2O3 makes use of constraints on special positions : 0,0,z for Al and x,0,1/4 for O. Such positions could be guessed knowing the chemical formula and being sure of the space group (this will not be always so easy...) (al2o3GP.zip) :
Al2O3 R-3c 4.764 4.764 13.009 90.0 90.0 120.0 R -3 C 1.54056 4 2 2 1 1 1 0.02511 -0.04562 0.03019 3 Al+3O-2 1 3.0 1.6 2.2 6. 6. 2. 1.0 0.002 5000 20000 20000 5000 0.2 2 10 1 0 <-- permutations are impossible in such a case 1 1 1.0 1 1 <-- nocc=1 and nspe =1 2. 3. 8 7 <-- codes for special positions 0,0,z and x,0,1/4In this way, a 100% success rate is ensured. This is because the number of degrees of freedom (DoF) is considerably reduced : 2 unknown parameters instead of 6. And the final result is :
Test number : 10 8-Apr-2000 Hour: 14 Min: 37 Sec: 59 ISEED = 297541756 67 moves acc. 19999 gen. and 16085 tested; R=0.006 0 perm. acc. 0 tested 19 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Al1 0.00000 0.00000 0.64791 2.000 O1 0.30602 0.00000 0.25000 3.000 8-Apr-2000 Hour: 14 Min: 38 Sec: 30 Final RF factor = 6.1535593E-03 Final Rp(F) factor = 6.0187900E-03
This example is a bit more complex with 4 independent atoms (12 DoF) (aragonite.zip) :
Aragonite CaCO3 4.961 7.967 5.741 90.00 90.00 90.00 P M C N 1.54056 4 4 3 1 1 1 0.02511 -0.04562 0.03019 3. Ca C O 0 4. 4. 4. 2 1.0 0.01 5000 60000 60000 20000 0.3 2 10 1 10 1 1 2 1.0 1 0 0.5 0.5 0.5 1.We should find :
Ca 0.25000 0.41508 0.24046 0.50000 C 0.25000 0.76211 0.08518 0.50000 O1 0.25000 0.92224 0.09557 0.50000 O2 0.47347 0.68065 0.08726 1.00000According to the formula and Z = 4, we know that Ca and C are necessarily on a special position of the Pmcn space group, with 4 equivalents. But the O atoms could either be distributed on one general plus one special or 3 specials. By chance ;-), the good choice was made here and the success rate is 8/10 :
Test number : 2 8-Apr-2000 Hour: 14 Min: 53 Sec: 21 ISEED = 322795864 450 moves acc. 54000 tested; Chi**2=0.437E-01, R=0.044 47 perm. acc. 5999 tested 191 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ca1 0.74481 0.91512 0.74000 0.500 C1 0.75189 0.26324 0.58666 0.500 O1 0.75234 0.07806 0.09336 0.500 O2 0.47217 0.81861 0.41180 1.000 8-Apr-2000 Hour: 15 Min: 25 Sec: 36 Final RF factor = 7.5921029E-02 Final Rp(F) factor = 4.3627698E-02You see that the occupation numbers were guessed but not the special positions. ESPOIR proposes positions close to the expected ones. To you to realize that 0.74, 0.91, 0.74 corresponds in fact to a special 1/4,y,z position in the Pmcn space group. You will also obtain identical proposals, different only by origin choice, displaced by 1/2 for instance.
This seems to be a rather simple example. However the success rate (3/50) is far from the Al2O3 success rate (8/10). Why ? There seem to be a lot of false minima with R~15% or higher (caf2.zip) :
CaF2 Fm3m 5.462 5.462 5.462 90.0 90.0 90.0 F M 3 M 1.54056 4 2 2 1 1 1 0.02511 -0.04562 0.03019 3. Ca+2F-1 0 6. 6. 2. 1. 0.002 5000 60000 60000 10000 0.1 2 50 1 10 1 1 1.0 1 0 0.5 1.The success rate would have been certainly enhanced if the special positions had been guessed.
12-Apr-2000 Hour: 17 Min: 7 Sec: 8 ISEED = 123257 0 moves acc. 0 tested; Chi**2=0.952 , R=0.952 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 178 moves acc. 54000 tested; Chi**2=0.951E-02, R=0.010 7 perm. acc. 5999 tested 73 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ca1 0.99584 0.49538 0.49572 0.500 F1 0.75988 0.25526 0.73676 1.000 12-Apr-2000 Hour: 17 Min: 9 Sec: 0 Final RF factor = 1.0959629E-02 Final Rp(F) factor = 9.5057748E-03Expected positions are :
Ca 0. 0. 0. F 1/4 1/4 1/4
This case is just a bit more complex than Al2O3, with the same space group (calcite.zip) :
Calcite CaCO3 4.990 4.990 17.061 90.0 90.0 120.0 R -3 C 1.54056 4 3 3 1 1 1 0.02511 -0.04562 0.03019 3. Ca C O 0 9. 9. 9. 2 1.0 0.002 5000 60000 10000 20000 0.3 2 10 1 10 1 1 1 1.0 1 0 0.166667 0.166667 0.5The expected result is :
Ca 0.00000 0.00000 0.00000 C 0.00000 0.00000 0.25000 O 0.25682 0.00000 0.25000Again, the good occupation numbers were guessed for the O atom, leading to a 2/10 success rate. Below is the result :
8-Apr-2000 Hour: 14 Min: 50 Sec: 11 ISEED = 311722348 0 moves acc. 0 tested; Chi**2=0.739 , R=0.739 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 205 moves acc. 54000 tested; Chi**2=0.376E-02, R=0.004 3 perm. acc. 5999 tested 62 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ca1 0.33468 0.66955 0.66667 0.167 C1 0.33275 0.66868 0.41423 0.167 O1 0.07638 0.41015 0.91888 0.500 8-Apr-2000 Hour: 14 Min: 55 Sec: 30
Final RF factor = 3.7637551E-03 Final Rp(F) factor = 3.7522253E-03Again, one has to retrieve special positions thinking to the R Bravais lattice.
Forsterite was for a while the most complex example found in the Endeavour package (but note that Endeavour worked only in P1, at the beginning, as well as ESPOIR), with up to 6 independent atoms (forsterite.zip) :
Forsterite Mg2SiO4 4.755 10.198 5.979 90.0 90.0 90.0 P B N M 1.54056 4 6 3 1 1 1 0.02511 -0.04562 0.03019 3. Mg+2Si+4O-2 0 5. 5. 5. 2. 1. 0.002 10000 100000 50000 40000 0.3 2 10 1 40 2 1 3 1.0 1 0 0.5 0.5 0.5 0.5 0.5 1.0And the expected result is :
Mg1 0.00000 0.00000 0.00000 0.50000 Mg2 0.99130 0.27730 0.25000 0.50000 Si 0.42610 0.09400 0.25000 0.50000 O1 0.76580 0.09190 0.25000 0.50000 O2 0.22100 0.44700 0.25000 0.50000 O3 0.27740 0.16300 0.03290 1.00000Miraculously, the true occupation number were guessed (but special positions were not forced to occur). The DoF is now of 18. And the result is obtained with a 3/10 success rate :
8-Apr-2000 Hour: 18 Min: 51 Sec: 59 ISEED = 149159323 0 moves acc. 0 tested; Chi**2=0.700 , R=0.700 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 307 moves acc. 97500 tested; Chi**2=0.172E-01, R=0.017 25 perm. acc. 2499 tested 33 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Mg1 0.50875 0.49923 0.00640 0.500 Mg2 0.50870 0.22264 0.75763 0.500 Si1 0.07374 0.40618 0.75599 0.500 O1 0.71996 0.94709 0.24252 0.500 O2 0.73394 0.40794 0.74355 0.500 O3 0.22193 0.33702 0.96654 1.000
8-Apr-2000 Hour: 19 Min: 16 Sec: 7 Final RF factor = 3.6787927E-02 Final Rp(F) factor = 1.7179536E-02
That's all for the Endeavour challenge
examples on the Endeavour side. Now the test files strictly from ESPOIR.
Li3RuO4 is cited a lot in the quite interesting book "Computer Modelling in Inorganic Crystallography" edited by C.R.A. Catlow (Academic Press). That structure was predicted in the P1 space group (programs GASPP + GULP), once TREOR gave a monoclinic cell proposition. The final space group (P2/a) was deduced from the structure proposition, and the structure refinement was done by GSAS (J. Mater Chem, 5, 1269, 1995).
Thus, the prediction (genetic algorithm) was not made by using a cost function involving the powder pattern.
It may be considered as strange that Li3RuO4 with 6 independent atoms in P2/a is qualified of "complex" in 1995, just after the structure of La3Ti5Al15O37 with 60 independent atoms is determined by classical powder methodology (structure factors extraction, direct method, see : J. Solid State Chem. 111 (1994) 52-57).
But of course, for a purely predictive attemp, it was really complex. Moreover, it is still probably out of the current true prediction possibilities (without the cell knowledge).
Anyway, Li3RuO4 would not have resisted more than 30 sec. to such a classical analysis. Even a Patterson would have revealed instantly the Ru position (see some discussion about this compound in the SDPD Mailing List).
ESPOIR is tested on that problem with large success rate whatever the space group (P1 with 16 atoms, P-1 with 8 atoms, or P2/a with 6 atoms).
In P1 (li3ruo40.zip) :
Li3RuO4 in P1 5.10555 5.85403 5.10587 90. 110.039 90. P 1 1.54056 4 16 3 1 1 1 0.02511 -0.04562 0.03019 3 Ru O Li 0 6. 6. 6. 2. 1. 0.002 10000 200000 50000 30000 0.2 2 10 1 10 2 8 6 1.0 0 0The success rate is 100% for R < 7%, and the best result is :
14-Apr-2000 Hour: 17 Min: 12 Sec: 49 ISEED = 123939 2855 moves acc. 180000 tested; Chi**2=0.132E-01, R=0.013 158 perm. acc. 19999 tested 952 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ru1 0.76209 0.65650 0.60958 1.000 Ru2 0.75202 0.38156 0.10876 1.000 O1 0.52550 0.62577 0.84202 1.000 O2 0.52080 0.90785 0.38040 1.000 O3 0.52531 0.62189 0.85341 1.000 O4 0.52886 0.62883 0.85440 1.000 O5 0.74367 0.09761 0.58699 1.000 O6 0.02295 0.87624 0.84094 1.000 O7 0.51977 0.90582 0.37901 1.000 O8 0.49850 0.38356 0.31750 1.000 Li1 0.73135 0.89480 0.06258 1.000 Li2 0.52049 0.13555 0.88285 1.000 Li3 0.52060 0.13471 0.88313 1.000 Li4 0.28207 0.00487 0.60878 1.000 Li5 0.53098 0.61823 0.97711 1.000 Li6 0.95342 0.18304 0.36798 1.000 14-Apr-2000 Hour: 17 Min: 27 Sec: 40 Final RF factor = 0.2549882 Final Rp(F) factor = 1.2715362E-02In P2/a (li3ruo4.zip), if you are able to guess the occupancy factors :
Li3RuO4 5.10555 5.85403 5.10587 90. 110.039 90. P 2/A 1.54056 4 6 3 1 1 1 0.02511 -0.04562 0.03019 3 Ru O Li 0 6. 6. 6. 2. 1. 0.002 5000 50000 25000 20000 0.2 2 10 1 10 1 2 3 1.0 1 0 0.5 1.0 1.0 0.5 0.5 0.5The success rate is 6/10 (R < 5%), and the best result is :
14-Apr-2000 Hour: 13 Min: 54 Sec: 55 ISEED = 100191 498 moves acc. 45000 tested; Chi**2=0.305E-01, R=0.030 3 perm. acc. 4999 tested 121 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ru1 0.75010 0.86017 0.99988 0.500 O1 0.97685 0.62935 0.24008 1.000 O2 0.00020 0.11553 0.23161 1.000 Li1 0.75014 0.53857 0.50018 0.500 Li2 0.78589 0.07139 0.52836 0.500 Li3 0.74919 0.40432 0.99952 0.500 14-Apr-2000 Hour: 14 Min: 7 Sec: 46 Final RF factor = 0.1645989 Final Rp(F) factor = 2.9407920E-02Note that RF is 16 % whereas Rp(F) = 2.9 %. This is indicating that there is strong overlapping, so that the extracted "|Fobs|" may be rather wrong but the regenerated powder pattern is still correct.
May be the Li atom positions are not really that good... This would need some checking by looking at the bond lenghts, and by making Fourier synthesis after the Rietveld refinements.
In order to illustrate the difference in behaviour of ESPOIR on the same problem if treated in P 1 and in P -1, the CuVO3 example already in the package (cuvo3c.dat) is approached here in P 1 (cuvo3.zip). We have now 10 atom sin general position, 30 DoF (degrees of freedom) :
Test on CuVO3 4.9646 5.4023 4.9154 90.32 119.13 63.93 P 1 1.54056 4 10 3 1 1 1 0.09 -0.03 0.04 0.04 Cu V O 0 3. 3. 3. 2. 1. 0.002 5000 100000 20000 20000 0.2 2 10 1 10 2 2 6 1.1 0 0And the result is :
8-Apr-2000 Hour: 16 Min: 35 Sec: 39 ISEED = 625767286 0 moves acc. 0 tested; Chi**2=0.627 , R=0.627 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 742 moves acc. 90000 tested; Chi**2=0.116E-02, R=0.001 26 perm. acc. 9999 tested 95 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Cu1 0.26821 0.27950 0.69056 1.000 Cu2 0.71098 0.13753 0.41304 1.000 V1 0.69989 0.64577 0.90675 1.000 V2 0.28232 0.77219 0.20265 1.000 O1 0.84023 0.93314 0.11733 1.000 O2 0.47274 0.94467 0.48335 1.000 O3 0.20911 0.94215 0.83917 1.000 O4 0.13166 0.48329 0.97418 1.000 O5 0.75580 0.47816 0.25396 1.000 O6 0.49573 0.47192 0.60955 1.000 8-Apr-2000 Hour: 17 Min: 12 Sec: 10 Final RF factor = 9.9563552E-04 Final Rp(F) factor = 7.1708602E-04The difference is that when an atom is moving, two atoms really move in P-1 according to a completely arbitrary origin. Generally, you will observe much less moves accepted in any space group than for the same problem described in P1. The problem is due (I think) to the impossibility to build a truly random starting model, excepted in P1. Anyway, ESPOIR do the job in 2 tests for 10 in P-1, to be compared to a succes rate of 5/10 in the P1 space group.
So, you may consider working in P1 sometimes.
This example is quite the more complex up to now, for two reasons : more atoms (16 in P 1; 48 degrees of freedom), and almost same diffusion factors for both atom types. If ESPOIR succeeds here, this should mean that organic materials at least as complex as TeI should be solved from scratch (random starting model) by ESPOIR. Again, you can compare the performances in P 1 and in P -1.
in P 1, with 16 atoms in general position, for 20 tests starting from different random models (tei.zip).
Test on TeI P1 9.958 7.992 8.212 104.4 90.1 102.9 P 1 1.54056 4 16 2 1 1 1 0.09 -0.04 0.03 3 Te I 0 5. 5. 2. 1. 0.005 5000 200000 40000 60000 0.35 2 20 1 10 8 8 1.0 0 0And the best result is :
9-Apr-2000 Hour: 11 Min: 3 Sec: 41 ISEED = 172661282 0 moves acc. 0 tested; Chi**2=0.577 , R=0.577 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 1418 moves acc. 180000 tested; Chi**2=0.187E-02, R=0.002 13830 perm. acc. 19999 tested 7215 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Te1 0.98675 0.47061 0.64021 1.000 Te2 0.37615 0.20524 0.82876 1.000 Te3 0.98642 0.47535 0.16504 1.000 Te4 0.37386 0.48026 0.64880 1.000 Te5 0.88995 0.19838 0.32841 1.000 Te6 0.46719 0.74408 0.95849 1.000 Te7 0.99622 0.74218 0.45772 1.000 Te8 0.38666 0.47760 0.12265 1.000 I1 0.64488 0.18281 0.82516 1.000 I2 0.01706 0.16947 0.79954 1.000 I3 0.24643 0.17128 0.33135 1.000 I4 0.72143 0.75655 0.45991 1.000 I5 0.11174 0.77039 0.95130 1.000 I6 0.74831 0.75964 0.96233 1.000 I7 0.61464 0.18266 0.32384 1.000 I8 0.35938 0.77403 0.48553 1.000 9-Apr-2000 Hour: 12 Min: 2 Sec: 1 Final RF factor = 3.1793690E-03 Final Rp(F) factor = 1.6125488E-03Almost each tested permutation is accepted. This is completely logical because of the Te and I diffusion factor similarities A total of 200000 events is sufficient, taking 1 hour on a Pentium II 266 Mhz (the 20 tests needing ~ 20 h - and this would be 5 h "only" on a Pentium III, 1 GHz). Only 200 reflections are sufficient for locating those 16 atoms. On would say that classical direct methods would have some difficulties if using the same limited data set. If the test had been directly on the "|Fobs|", a reduction of time by a factor 5 would have been obtained.
In P -1, the above success rate (12/20 if one considers that R < 15 % is successful) is reduced by a factor 2, but ESPOIR still works (teic.zip).
Test on TeI P-1 9.958 7.992 8.212 104.4 90.1 102.9 P -1 1.54056 4 8 2 1 1 1 0.09 -0.04 0.03 3 Te I 0 5. 5. 2. 1. 0.005 5000 200000 40000 60000 0.35 2 20 1 10 4 4 1.0 0 0After 20 cycles, 3 runs give R<20%, and the result is :
13-Apr-2000 Hour: 16 Min: 28 Sec: 41 ISEED = 118643 551 moves acc. 180000 tested; Chi**2=0.163 , R=0.163 11449 perm. acc. 19999 tested 5978 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Te1 0.12008 0.76924 0.56686 1.000 Te2 0.33474 0.49978 0.75723 1.000 Te3 0.65572 0.51429 0.76373 1.000 Te4 0.94702 0.79182 0.55014 1.000 I1 0.60855 0.23108 0.93971 1.000 I2 0.04512 0.79243 0.06616 1.000 I3 0.53488 0.80618 0.57444 1.000 I4 0.27835 0.22808 0.91966 1.000 13-Apr-2000 Hour: 16 Min: 50 Sec: 25 Final RF factor = 0.3050798 Final Rp(F) factor = 0.1634225No proposal gives the complete structure. This shows again how ESPOIR is more efficient in P 1 in scratch mode. In fact, one should try 50 runs and see what happen. Anyway, a part of the structure is there and it could be completed by running the Rietveld method, and then performing a Fourier difference synthesis.
Clearly, one should not expect that Te and I are really well differentiated here (they are not, of course). So that looking at interatomic distances would allow to recognize Te and I atoms (no I-I direct contact, but Te-I and Te-Te are allowed).
In P1, instead of Pnma, there are 24 independent atoms in the cell. The large success rate below (20/20 have R < 10%) is certainly due to easy location of the 4 heavy Pb scatterers. Anyway, in the best solutions, also the S and many of the O atoms were located (pbso4p1.zip).
Test on PbSO4 P1 instead of Pnma 8.482 5.398 6.959 90. 90. 90. P 1 1.54056 4 24 3 1 1 1 0.02511 -0.04562 0.03019 3 Pb S O 0 5. 5. 5. 2. 1. 0.001 20000 500000 100000 40000 0.3 2 20 1 10 4 4 16 1.0 0 0The best result is :
11-Apr-2000 Hour: 12 Min: 16 Sec: 26 ISEED = 304158790 0 moves acc. 0 tested; Chi**2=0.575 , R=0.575 0 perm. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 4424 moves acc. 450000 tested; Chi**2=0.211E-01, R=0.021 152 perm. acc. 49999 tested 1413 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Pb1 0.29802 0.15914 0.90542 1.000 Pb2 0.67726 0.65837 0.24710 1.000 Pb3 0.17507 0.66032 0.41167 1.000 Pb4 0.80505 0.15734 0.73674 1.000 S1 0.55053 0.65643 0.76481 1.000 S2 0.41515 0.16088 0.39717 1.000 S3 0.04000 0.66245 0.89509 1.000 S4 0.92705 0.16186 0.26378 1.000 O1 0.56092 0.16241 0.49745 1.000 O2 0.66830 0.66712 0.63038 1.000 O3 0.90561 0.93205 0.38221 1.000 O4 0.90139 0.67454 0.97128 1.000 O5 0.75823 0.16374 0.74527 1.000 O6 0.90664 0.38514 0.37606 1.000 O7 0.78759 0.15706 0.12146 1.000 O8 0.88849 0.62166 0.96959 1.000 O9 0.57367 0.87384 0.88338 1.000 O10 0.38835 0.66059 0.68514 1.000 O11 0.41223 0.94241 0.26844 1.000 O12 0.06731 0.87237 0.77188 1.000 O13 0.57894 0.43859 0.86794 1.000 O14 0.19339 0.65827 0.08272 1.000 O15 0.42180 0.37891 0.26055 1.000 O16 0.29632 0.14576 0.52368 1.000 11-Apr-2000 Hour: 15 Min: 31 Sec: 32 Final RF factor = 8.2848787E-02 Final Rp(F) factor = 2.1060312E-02
Working in P1 needs
then to determe the space group, and to find a new origin, if any.
Finding symmetry elements can then be attempted by using PLATON on the name.spf output :
TITL Test on PbSO4 CELL 8.4820 5.3980 6.9590 90.0000 90.0000 90.0000 SPGR P1 ATOM pb1 0.42876 0.65290 0.18283 ATOM pb2 0.81621 0.16184 0.49586 ATOM pb3 0.31170 0.14734 0.69931 ATOM pb4 0.93629 0.65219 0.02093Testing with PLATON the above .spf file containing only the Pb atoms as proposed by ESPOIR is sufficient to retrieve the true space group (Pnma) :
Conventional, New or Pseudo Symmetry ========================================================== Space Group Pnma No: 62, Laue: mmm [Hall: -P 2ac 2n ] Lattice Type oP, Centric, Orthorhombic, Order 8( 4) [Shoenflies: D2h^16 ] Nr ***** Symmetry Operation(s) ***** 1 X , Y , Z 2 1/2 - X , - Y , 1/2 + Z 3 1/2 + X , 1/2 - Y , 1/2 - Z 4 - X , 1/2 + Y , - Z 5 - X , - Y , - Z 6 1/2 + X , Y , 1/2 - Z 7 1/2 - X , 1/2 + Y , 1/2 + Z 8 X , 1/2 - Y , Z :: Origin shifted to:-0.122,-0.407, 0.339 after transformation
In the case of CuVO3 and
TeI, the best ESPOIR propositions are almost fully correct in P1 space
group, so that PLATON has no difficulty to locate the inversion
center (the true structures are both P-1) from the whole atomic positions,
provided the I atoms are labelled also Te, in the hypothesis of some misplacement.
Concerning PbSO4, if you want to apply ESPOIR in the right Pnma space group, the problem is of course to decide which and how many atoms are on special positions. With Z = 4, there is little doubt that Pb and S are on special positions, but the question is for the O atoms. You can postulate that, owing to the Pb weight, this will not be important and try all atoms in general position (this wrong choice will only have a small influence on the scale factor).
The two ways to run the PbSO4 test case, either in automatic mode (all atoms at general positions) (pbso4.zip), or by guessing if atoms could be on special positions (pbso41.zip), are shown below.
Test on PbSO4 Pnma 8.482 5.398 6.959 90. 90. 90. P N M A 1.54056 4 5 3 1 1 1 0.02511 -0.04562 0.03019 3 Pb S O 0 5. 5. 5. 2. 1. 0.002 5000 100000 20000 20000 0.2 2 10 1 10 1 1 3 1.0 0 0 <-- all atoms with occupancy factor =1 and in general position
The 10 tests produce 7 success with
R < 10 %. The best result is below:
8-Apr-2000 Hour: 23 Min: 22 Sec: 57 ISEED = 495891907 517 moves acc. 90000 tested; Chi**2=0.442E-01, R=0.044 12 perm. acc. 9999 tested 144 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Pb1 0.68743 0.24959 0.33311 1.000 S1 0.93711 0.76917 0.31308 1.000 O1 0.68740 0.24954 0.95111 1.000 O2 0.59252 0.75118 0.10290 1.000 O3 0.58156 0.04751 0.69420 1.000 8-Apr-2000 Hour: 23 Min: 49 Sec: 54 Final RF factor = 4.9446784E-02 Final Rp(F) factor = 4.4187289E-02
The starting pbso41.dat file, with
true occupancy numbers is below :
Test on PbSO4 Pnma 8.482 5.398 6.959 90. 90. 90. P N M A 1.54056 4 5 3 1 1 1 0.02511 -0.04562 0.03019 3 Pb S O 0 5. 5. 5. 2. 1. 0.002 5000 100000 20000 20000 0.2 2 10 1 10 1 1 3 1.0 1 0 0.5 0.5 1. 0.5 0.5The success rate is 8/10 for R < 10%, and the best result is :
13-Apr-2000 Hour: 15 Min: 43 Sec: 48 ISEED = 113257 366 moves acc. 90000 tested; Chi**2=0.140E-03, R=0.000 67 perm. acc. 9999 tested 93 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Pb1 0.18790 0.75167 0.33330 0.500 S1 0.43670 0.25002 0.31581 0.500 O1 0.41800 0.47401 0.19099 1.000 O2 0.19400 0.75195 0.95699 0.500 O3 0.90800 0.75021 0.90402 0.500 13-Apr-2000 Hour: 15 Min: 54 Sec: 48 Final RF factor = 1.4865046E-04 Final Rp(F) factor = 1.3130555E-04A last test would have consisted in trying to guess also the special positions occupied by the Pb and S atoms (which is not really difficult in the Pnma space group).
This compound structure is solved in Im2m, however all the other possible groups had to be tried. This example illustrates a more complicated manual choice of the occupation numbers (im2m.zip), impossible if you do not have the right chemical formula.
Ba2CdP3O10(OH) Im2m 11.9031 7.3407 5.5533 90.0 90.0 90.0 I M 2 M 1.54056 4 9 4 1 1 1 0.07084 -0.04479 0.02767 3 Ba Cd P O 0 6. 6. 6. 6. 2. 1.0 0.002 5000 60000 20000 20000 0.3 2 10 1 10 1 1 2 5 1.0 1 0 0.5 0.25 0.5 0.25 1.0 0.5 0.5 0.5 0.25The success rate is 5/10 for R<15%. The best result is :
8-Apr-2000 Hour: 19 Min: 50 Sec: 9 ISEED = 145909755 709 moves acc. 54000 tested; Chi**2=0.670E-01, R=0.067 188 perm. acc. 5999 tested 281 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers Ba1 0.69473 0.89495 0.49064 0.500 Cd1 0.99989 0.67059 0.49745 0.250 P1 0.89274 0.87620 0.99962 0.500 P2 0.00065 0.25397 0.50025 0.250 O1 0.86880 0.74861 0.79438 1.000 O2 0.65248 0.52056 0.49967 0.500 O3 0.70287 0.57708 0.96223 0.500 O4 0.99972 0.37149 0.72250 0.500 O5 0.50048 0.19876 0.00473 0.250 8-Apr-2000 Hour: 20 Min: 18 Sec: 20 Final RF factor = 8.0833592E-02 Final Rp(F) factor = 6.6992961E-02Many of the true positions are special positions with 0 or 1/2 coordinates. You should not expect that ESPOIR will give you such exact values. You will have to give a look to the International Table for Crystallography.
In such a case, the automatic mode (all atoms in general position) will not work, unless you try in P1 space group ! Can you easily guess those occupation numbers ? Not for all the oxygen atoms but there is not a lot of possibilities for the Ba, Cd and P atoms, so that a part of the solution is attainable, at least.
Fortunately, many space groups do not present any special positions, or many organic compounds show all their atoms in general position (like the cimetidine in P21/n - last scratch example below).
Ahem, note that the final structure of Ba2CdP3O10(OH) was found distorted in the monoclinic system, with beta=90.09°...
In all the previous examples, the structure factors presented to ESPOIR were excellent ones (as provided by a single crystal study). The present case is the SDPD round robin sample I, for which no participant proposed a model (although it was solved by the organizers, see : Solid State Sciences 1, 1999, 55-62). Below is shown the ESPOIR performance on this compound with good data and with selected "|Fobs|" extracted from the Round Robin X-ray pattern.
- Good data in P 1.
ESPOIR works fine for this 30 atoms problem,
but you will have to apply PLATON for searching the missing symmetry operators,
and some atoms are certainly misplaced or not well identified. Have a look
at the 2 Co aoms related by a y+1/2 translation, which is a good sign :
640 moves acc. 1981001 tested; Chi**2=0.783E-01, R=0.078 22227 perm. acc. 198100 tested 10743 events did not improved the fitFinal coordinates x,y,z and occupation numbers
co 1 0.08745 0.07298 0.55174 1.000 co 2 0.73690 0.57190 0.43416 1.000 n 1 0.11759 0.56399 0.53891 1.000 n 2 0.72046 0.12305 0.95530 1.000 n 3 0.65802 0.71939 0.60319 1.000 n 4 0.81151 0.43511 0.25895 1.000 n 5 0.82421 0.44626 0.66004 1.000 n 6 0.10960 0.62280 0.02686 1.000 n 7 0.66342 0.70737 0.19529 1.000 n 8 0.34270 0.98788 0.61994 1.000 n 9 0.16966 0.20956 0.79560 1.000 n 10 0.47434 0.48721 0.35990 1.000 n 11 0.17457 0.22209 0.37140 1.000 n 12 0.01310 0.94498 0.32230 1.000 c 1 0.01814 0.94085 0.73032 1.000 c 2 0.14872 0.06910 0.54082 1.000 o 1 0.85626 0.20192 0.98168 1.000 o 2 0.31789 0.98017 0.11658 1.000 o 3 0.24503 0.69159 0.54010 1.000 o 4 0.71507 0.00071 0.87474 1.000 o 5 0.56270 0.19712 0.95573 1.000 o 6 0.27031 0.69413 0.03566 1.000 o 7 0.57408 0.18812 0.46404 1.000 o 8 0.16760 0.47710 0.60812 1.000 o 9 0.96780 0.70361 0.02286 1.000 o 10 0.11143 0.49537 0.11406 1.000 o 11 0.66362 0.99035 0.37812 1.000 o 12 0.50667 0.47603 0.88218 1.000 o 13 0.83425 0.17602 0.44959 1.000 o 14 0.99477 0.67122 0.53212 1.000
- Good data in P21.
This is more direct :
344 moves acc. 1981123 tested; Chi**2=0.365E-01, R=0.037 15846 perm. acc. 198112 tested 7769 events did not improved the fitFinal coordinates x,y,z and occupation numbers
co 1 0.81950 0.23785 0.93907 1.000 n 1 0.74516 0.10563 0.69804 1.000 n 2 0.89369 0.37553 0.76021 1.000 n 3 0.26168 0.59025 0.88503 1.000 n 4 0.09917 0.87128 0.82629 1.000 n 5 0.80493 0.69140 0.46587 1.000 n 6 0.56948 0.32317 0.87206 1.000 c 1 0.79570 0.70602 0.94995 1.000 o 1 0.34462 0.11217 0.53715 1.000 o 2 0.74427 0.83145 0.88826 1.000 o 3 0.07663 0.13665 0.04575 1.000 o 4 0.59402 0.33707 0.37846 1.000 o 5 0.05891 0.11206 0.51844 1.000 o 6 0.79752 0.81448 0.38107 1.000 o 7 0.34391 0.11612 0.04028 1.000The success rate is here of 4/40 and 17 hours of calculation on a Pentium II 266 MHz, and the structure is almost perfect, no error on C, N and O assignments...
Now, if we examine the result with real data, as extracted from the powder pattern distributed with the SDPD Round Robin, the result is certainly not as beautiful. The "|Fobs|" were extracted by the Le Bail method with Fullprof. Near of 150 reflections (at the lowest angles) are used (for 15 atoms to be found in P21). Below are the best results :
179 moves acc. 1980792 tested; Chi**2=0.193 , R=0.193 5133 perm. acc. 198079 tested 2639 events did not improved the fitFinal coordinates x,y,z and occupation numbers
co 1 0.82093 0.36020 0.94044 1.000 n 1 0.37594 0.07268 0.14666 1.000 n 2 0.62631 0.90305 0.47297 1.000 n 3 0.83421 0.84308 0.44808 1.000 n 4 0.37878 0.39791 0.31452 1.000 n 5 0.78679 0.38652 0.44956 1.000 n 6 0.69884 0.09903 0.45740 1.000 c 1 0.16988 0.23056 0.21554 1.000 o 1 0.79673 0.36041 0.97713 1.000 o 2 0.63487 0.91408 0.05895 1.000 o 3 0.43222 0.33256 0.09743 1.000 o 4 0.43146 0.66930 0.73072 1.000 o 5 0.40683 0.95036 0.59913 1.000 o 6 0.78341 0.77434 0.91579 1.000 o 7 0.74343 0.48008 0.05556 1.000This is not a complete solution but many atoms are already well placed, including the Co atom.
The success rate is of the order of 1/50. The best result is shown below with R = 3.7% after 8000000 moves and 7 hours of calculation (Pentium II 266Mhz). If you dispose of a big and powerful computer, try to do more tests on it, and let me know the result.
432 moves acc. 7990498 tested; Chi**2=0.372E-01, R=0.037 15679 perm. acc. 799049 tested 7894 events did not improved the fitFinal coordinates x,y,z and occupation numbers
s 1 0.98255 0.91396 0.69786 1.000 c 1 0.08635 0.83805 0.07537 1.000 c 2 0.64513 0.60618 0.14642 1.000 c 3 0.06324 0.65779 0.72502 1.000 c 4 0.72905 0.74969 0.67829 1.000 c 5 0.12604 0.54853 0.25767 1.000 c 6 0.90039 0.78266 0.20823 1.000 c 7 0.03221 0.78999 0.16923 1.000 c 8 0.46558 0.90546 0.90365 1.000 c 9 0.47914 0.41234 0.50753 1.000 c 10 0.73601 0.53650 0.28145 1.000 n 1 0.87490 0.26547 0.77556 1.000 n 2 0.40569 0.09148 0.11088 1.000 n 3 0.29048 0.31663 0.43408 1.000 n 4 0.33178 0.01164 0.35182 1.000 n 5 0.95375 0.62665 0.56134 1.000 n 6 0.63445 0.05413 0.25410 1.000
The success rate is 100% for this rather simple case. The C60 molecule is orientationally disordered, the scattering factor is a global one, corresponding to a sphere with appropriate radius (taken from the Fullprof test files). The space group is Fm3m and the molecule has just to be found at the 0,0,0 position. The data are given in a special way (with a negative nt value), with scattering factors as couples of X*sintheta/lamda, (global scattering factor)/Y, and a first line giving the number of couples (57) and the X and Y scales (c60.zip) :
Test on C60 Fm3m 14.152000 14.152000 14.152000 90.000000 90.000000 90.000000 F M 3 M 0.7073 4 1 -1 1 0 1 <--- nt is negative C 57 2000. 1. 0.000 1.00000 22.599 0.95840 45.198 0.83990 67.797 0.66190 90.396 0.45010 112.994 0.23400 135.593 0.04170 158.192 -0.10450 180.791 -0.19150 203.390 -0.21710 225.989 -0.18930 248.588 -0.12390 271.186 -0.04140 293.785 0.03790 316.384 0.09720 338.983 0.12610 361.582 0.12220 384.181 0.09030 406.780 0.04080 429.379 -0.01300 451.977 -0.05840 474.576 -0.08570 497.175 -0.09030 519.774 -0.07310 542.373 -0.04010 564.972 -0.00010 587.571 0.03670 610.169 0.06210 632.768 0.07090 655.367 0.06210 677.966 0.03910 700.565 0.00820 723.164 -0.02280 745.763 -0.04640 768.362 -0.05750 790.961 -0.05410 813.559 -0.03790 836.158 -0.01350 858.757 0.01290 881.356 0.03480 903.955 0.04730 926.554 0.04770 949.153 0.03660 971.751 0.01720 994.350 -0.00550 1016.949 -0.02590 1039.548 -0.03910 1062.147 -0.04230 1084.746 -0.03510 1107.345 -0.01970 1129.943 -0.00010 1152.542 0.01870 1175.141 0.03220 1197.740 0.03750 1220.339 0.03340 1242.938 0.02140 1265.537 0.00460 0 9.0 2. 1. 0.005 1000 20000 20000 20000 0.40 2 10 1 0 1 7. 0 0And the result is (using the first 50 hkl) :
7-Apr-2000 Hour: 19 Min: 15 Sec: 28 ISEED = 254537710 Starting coordinates x,y,z and occupation numbers c1 0.31757 0.18924 0.77633 1.000 189 moves acc. 19999 tested; Chi**2=0.613E-01, R=0.061 0 perm. acc. 0 tested 81 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers c1 0.51075 0.48959 0.98909 1.000 7-Apr-2000 Hour: 19 Min: 18 Sec: 6This result gives nearly 1/2,1/2,0, which is one of the F-centered positions equivalent to 0,0,0.
This compound was used as an example for the GAP program (Genetic Algorithm Program, still unavailable) (Zeit. Kristallogr. 212, 1997, 550-552). By GAP, a solution for the whole C16D10 molecule (ToF neutron data) could be obtained in 33 seconds.
ESPOIR is not able to do as well when working on the regenerated powder pattern (see time below, though, if working on the "|Fobs|", the time would become similar to the GAP time).
The C16 group is here located from X-ray data . The success rate is 100% for R values < 10%, for 10 tests, (pyrene.zip) :
Test on Pyrene 13.649 9.256 8.470 90.0 100.28 90.0 P 21/A 1.52904 4 16 1 1 1 1 0.02511 -0.04562 0.03019 3 C 0 7. 2. 1. 0.002 5000 80000 80000 40000 0.35 2 10 2 4 16 3.0 0 0 0.00 0.00 0.00 90.0 90.0 90.0 <-- Cartesian coordinates 4.2223 -0.3721 3.4328 1.00 4.6117 0.2277 2.2644 1.00 3.9412 -0.0713 1.0618 1.00 4.2967 0.5248 -0.1984 1.00 3.6721 0.2194 -1.3151 1.00 2.5940 -0.6831 -1.3384 1.00 1.8878 -1.0209 -2.5169 1.00 0.8355 -1.9345 -2.4719 1.00 0.4684 -2.5417 -1.3284 1.00 1.1167 -2.2177 -0.1092 1.00 0.7541 -2.8416 1.1301 1.00 1.3758 -2.5658 2.2552 1.00 2.4843 -1.6059 2.2694 1.00 3.1909 -1.3069 3.4678 1.00 2.8695 -1.0098 1.0859 1.00 2.1862 -1.3042 -0.1133 1.00The Cartesian coordinates were taken from the Cambridge Structural Databank (CSD), here recognized by putting a = b = c = 0.
The time for testing 60000 rotations and 20000 translations per run (50 "|Fobs|" used for building the regenerated powder pattern) was 12 mn on a Pentium II 266MHz (for one run). The best result is :
8-Apr-2000 Hour: 22 Min: 10 Sec: 15 ISEED = 591138599 0 rot. acc. 0 tested; Chi**2=0.563 , R=0.563 0 trans. acc. 0 tested 0 events did not improved the fit, DUMP = 1.000000 1182 rot. acc. 60000 tested; Chi**2=0.668 , R=0.073 39 trans. acc. 19999 tested 409 events did not improved the fit, DUMP = 0.000000 Final coordinates x,y,z and occupation numbers C1 0.78352 0.96163 0.91066 1.000 C2 0.70721 0.86742 0.91901 1.000 C3 0.63974 0.83043 0.77881 1.000 C4 0.55818 0.73202 0.77907 1.000 C5 0.49502 0.70031 0.64736 1.000 C6 0.50501 0.75783 0.49740 1.000 C7 0.43934 0.72462 0.35305 1.000 C8 0.45293 0.78663 0.20850 1.000 C9 0.52684 0.88116 0.20073 1.000 C10 0.59651 0.91580 0.34078 1.000 C11 0.67632 0.01588 0.33746 1.000 C12 0.73953 0.05071 0.46788 1.000 C13 0.72925 0.98808 0.62312 1.000 C14 0.79546 0.02586 0.76665 1.000 C15 0.65197 0.89352 0.63013 1.000 C16 0.58517 0.85588 0.48906 1.000 8-Apr-2000 Hour: 22 Min: 22 Sec: 58 Final RF factor = 0.1104051 Final Rp(F) factor = 7.2803810E-02
The structure of the RKSA1 monosaccharide C13H20N2O5 was recently predicted (L. Smrcok, M. Durik & D. Tunega, Z. Kristallogr. 215, 2000, 254-259) by using the HARDPACK program. In that process, no powder diffraction data is used, an energy minimum is searched for packing configurations of known molecules. Knowing the cell and/or the space group is not an obligation in that technique, but it may help a lot (the cell and space group knowledge was included in the above referenced work, predicting a structure previously determined from single crystal data by using the direct methods - B. Steiner, M. Koos, V. Langer, D. Gyepesova & L. Smrcok, Carbohydrate Res. 311, 1998, 1-9)). The powder diffraction data may be used as a final test for the proposed solution.
Applying ESPOIR to the 50 first structure factor amplitudes extracted from the powder pattern, the RKSA1 molecule was easily located. The success rate is 40-80 % for Rp(F) < 13 %, either using torsion angles or not (rksa1.zip) :
Without freeing the torsion angles (rksa1.dat) :
! title RKSA1 ! a, b, c, alpha, beta, gamma 8.7686 8.6510 10.0030 90.0 103.833 90.0 ! space group P 21 ! lambda, radiation, N of atoms, types of atoms, N of objects, ! "|Fobs|" or patterns, iprint 1.78892 4 40 4 1 1 5 0.10000 -0.01912 0.01836 3 ! atom names, in 8A4 C H N O ! code for minimal distance contraints 0 ! maximum moves for each type of atom 10.000 10.000 10.000 10.000 ! annealing law, sigma, reject 1.0000 1.0000 0.0050 ! number of events for : print, maximum, save 10000 100000 100000 ! events for restart, rmax, ichi, number of runs 50000 0.400 2 10 ! object type and NPERM for object 1 2 4 ! number of atoms of each type in object 1 13 20 2 5 ! B overall, NOCC, NSPE for object 1 4.0 0 0 ! cell parameters, and x, y, z, occup. for object 1 !Add there the cell parameters ! and the x,y,z, occup. for your object 1 0.0 0.0 0.0 90.000 90.000 90.000 1.28649 1.51081 -1.09543 1.0 1.70731 0.39245 -0.14634 1.0 0.73658 0.09456 0.98608 1.0 -0.76365 0.23464 0.56115 1.0 -0.89683 1.61475 -0.14282 1.0 1.91698 -1.81374 0.32282 1.0 1.52353 3.87008 -1.22846 1.0 3.33699 -1.88972 0.82641 1.0 1.38502 -3.15958 -0.08199 1.0 -2.40164 -1.33363 -0.49612 1.0 -2.53843 -2.4155 -1.53132 1.0 -1.53043 0.19662 1.82091 1.0 -2.30251 1.98313 -0.56142 1.0 -0.5034 -1.22275 -0.80844 1.0 1.77113 1.40845 -1.96375 1.0 2.59846 0.62092 0.24509 1.0 0.92301 0.70809 1.75323 1.0 -0.52826 2.32905 0.45154 1.0 1.95452 4.63023 -0.78412 1.0 0.5618 4.04186 -1.31068 1.0 1.91148 3.74975 -2.12028 1.0 3.36786 -2.4425 1.63478 1.0 3.65813 -0.98745 1.03431 1.0 3.9067 -2.28836 0.13592 1.0 1.39812 -3.76189 0.69146 1.0 1.94611 -3.53135 -0.79415 1.0 0.46536 -3.06399 -0.40575 1.0 -1.65462 -2.62956 -1.89823 1.0 -3.12441 -2.10556 -2.25275 1.0 -2.92304 -3.21635 -1.11835 1.0 -2.89157 1.9688 0.22253 1.0 -2.62621 1.33607 -1.22343 1.0 -2.30249 2.88084 -0.95409 1.0 -1.14311 -0.84952 -0.33302 1.0 -1.96606 0.25054 2.87958 1.0 1.73199 2.67666 -0.44912 1.0 -3.35361 -0.92144 0.15549 1.0 1.06231 -1.23843 1.35516 1.0 1.79598 -0.88863 -0.7825 1.0 -0.1086 1.53234 -1.33663 1.0The best result is :
Object number 1 at test 5. Previous min R=0.097 at test 3 0 rot. acc. 0 gen. ; Chi**2=0.692 , R=0.692 0 trans. acc. 0 tested 0 events did not improve the fit, DAMP = 1.000000 Object number 1 at test 5. Previous min R=0.097 at test 3 10 rot. acc. 9409 gen. ; Chi**2=0.105 , R=0.105 9 trans. acc. 3136 tested 1 events did not improve the fit, DAMP = 0.874560 Object number 1 at test 5. Previous min R=0.096 at test 5 12 rot. acc.75000 gen. ; Chi**2=0.286 , R=0.096 19 trans. acc.24999 tested 4 events did not improve the fit, DAMP = 0.009980The data (see rksa2.dat in the zipped file) treated with free torsion angles (automatic location of the rotatable bonds) differs from the above data file by a nobt=-3 line, requiring an optional subsequent line in which the maximum rotation angles are given (360° for the whole molecule, and 5° for the torsion angles) :
! object type and NPERM for object 1 -3 4 360. 5.The .xyz files including the accepted Monte Carlo events are in the rksa1.zip file. If your Web browser is completed by the CHIME plug-in, you should see below the starting model, and the animation up to the final model, by clicking on the mouse right button, and selecting "animation" :
Below is the ball and stick static display
of the 2 molecules in the cell
(cell outline unfortunately not represented
by CHIME) :
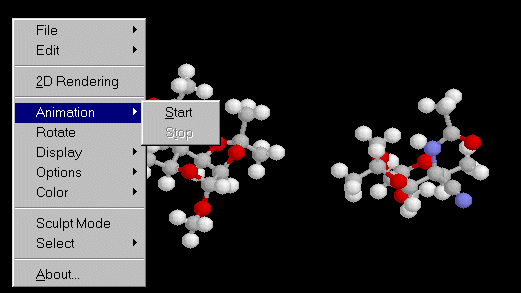
Note that the success ratio is better without
torsion angles in that case... This is because the exact molecule is used
as starting model.
The structure of this compound was determined by the OCTOPUS-96 program (still unavailable on the Internet, Monte Carlo approach) (Mater. Chem. 6, 1996, 1601-1604). The solution was from a C13 fragment at move 18251 in a run of 20000 events, with Rwp = 33.7%.
Analogous conditions were used here, with the C13 fragment defined in ESPOIR as object one, however the 14th C atom could be considered as object two. Only the 50 first extracted "|Fobs|" were retained for building the regenerated powder pattern. Ten runs were realized, for 100000 Monte Carlo events per run (50000 events for each object, 37500 rotations + 12500 translations for object one, and 50000 moves for object two) (methyl.zip).
Test on 1-methylfluorene : C13 + C 14.297300 5.701100 12.3733 90.00 95.1060 90. P 21/N 1.52904 4 14 1 2 1 1 <-- two objects 0.02511 -0.04562 0.03019 3 C 0 7. 2. 1.0 0.005 5000 100000 100000 50000 0.25 2 20 2 4 13 3.5 0 0 14.297300 5.701100 12.3733 90.00 95.1060 90. 0.29800 1.24300 -0.03500 1.00 0.37100 1.08300 -0.04400 1.00 0.39900 0.91000 0.03700 1.00 0.33900 0.86300 0.11900 1.00 0.26500 1.01800 0.12500 1.00 0.19700 1.02800 0.20900 1.00 0.18600 0.88300 0.29700 1.00 0.11300 0.93100 0.36300 1.00 0.05300 1.12000 0.33600 1.00 0.06100 1.25900 0.24400 1.00 0.13500 1.21300 0.18300 1.00 0.16300 1.52200 0.08400 1.00 0.24300 1.20000 0.05000 1.00 1 0 <-- the second object is just one C atom at random 1 3.5 0 0The success rate is 12/20 for R < 10%. And the best result obtained in 16 minutes, on a Pentium II 266MHz, is :
7-Apr-2000 Hour: 18 Min: 49 Sec: 12 ISEED = 436862952 Object number 1 506 rot. acc. 37593 tested; Chi**2=0.525E-01, R=0.052 42 trans. acc. 12530 tested 440 events did not improved the fit, DUMP = 0.000006 Object number 2 40 moves acc. 49876 tested; Chi**2=0.525E-01, R=0.052 0 perm. acc. 0 tested 14 events did not improved the fit, DUMP = 0.000006 Final coordinates x,y,z and occupation numbers C1 0.19850 0.13409 0.46451 1.000 C2 0.26989 0.96925 0.45613 1.000 C3 0.29616 0.79634 0.53779 1.000 C4 0.23572 0.75509 0.61995 1.000 C5 0.16329 0.91494 0.62535 1.000 C6 0.09541 0.93121 0.70929 1.000 C7 0.08298 0.78897 0.79784 1.000 C8 0.01048 0.84316 0.86364 1.000 C9 0.95238 0.03534 0.83591 1.000 C10 0.96176 0.17169 0.74338 1.000 C11 0.03527 0.11955 0.68258 1.000 C12 0.06633 0.42439 0.58241 1.000 C13 0.14310 0.09658 0.54966 1.000 C1 0.82325 0.64989 0.61123 1.000 7-Apr-2000 Hour: 19 Min: 5 Sec: 13 Final RF factor = 8.3380125E-02 Final Rp(F) factor = 5.2450635E-02
If you knew the cimetidine molecule shape, could you locate it, as well as the S atom, by using ESPOIR version 3 ? Undoubtedly yes (cim0.zip) :
Test on cimetidine C10H16N6S : C10N6 + S 10.7001 18.8206 6.8255 90.0 111.28 90.0 P 21/N 1.52904 4 17 3 2 1 1 0.01176 -0.00481 0.00223 3. S C N 0 7. 7. 7. 2. 1. 0.005 5000 100000 100000 40000 0.35 2 20 2 4 <-- object number one, the C10N6 rigid fragment 0 10 6 3.0 0 0 10.7001 18.8206 6.8255 90.0 111.28 90.0 0.23174 0.35195 0.77730 1.0000 0.08631 0.43676 0.67645 1.0000 0.02869 0.38828 0.76868 1.0000 -0.10273 0.38175 0.80964 1.0000 0.02448 0.51120 0.59391 1.0000 0.14323 0.49332 0.24463 1.0000 0.23598 0.56322 0.37858 1.0000 0.46070 0.50489 0.50155 1.0000 0.56444 0.44226 0.82692 1.0000 0.62392 0.54993 0.35794 1.0000 0.45268 0.47273 0.66131 1.0000 0.21030 0.41723 0.66634 1.0000 0.36874 0.54625 0.34632 1.0000 0.12808 0.33514 0.82688 1.0000 0.59352 0.50863 0.49126 1.0000 0.66651 0.58746 0.25019 1.0000 1 0 <-- object number 2 : the S atom at random 1 0 0 3.0 0 0The success rate is 4/20 for R < 15 % (100000 Monte Carlo events : 37500 rotations + 12500 translations for object one, 50000 moves for the S atom - object two), using the first 50 extracted "|Fobs|" for regenerating the powder pattern. The best result is :
7-Apr-2000 Hour: 19 Min: 53 Sec: 54 ISEED = 282762188 Object number 1 437 rot. acc. 37288 tested; Chi**2=0.910E-01, R=0.091 17 trans. acc. 12429 tested 290 events did not improved the fit, DUMP = 0.000032 Object number 2 69 moves acc. 50282 tested; Chi**2=0.910E-01, R=0.091 0 perm. acc. 0 tested 1 events did not improved the fit, DUMP = 0.000032 Final coordinates x,y,z and occupation numbers C1 0.72529 0.25855 0.19659 1.000 C2 0.57760 0.34087 0.06691 1.000 C3 0.51791 0.29541 0.16436 1.000 C4 0.38333 0.29063 0.19617 1.000 C5 0.51467 0.41300 0.96386 1.000 C6 0.64670 0.38480 0.63521 1.000 C7 0.73439 0.45785 0.75661 1.000 C8 0.96105 0.40221 0.90757 1.000 C9 0.05870 0.34852 0.24856 1.000 C10 0.12974 0.44233 0.76856 1.000 N1 0.94913 0.37470 0.07093 1.000 N2 0.70460 0.32058 0.07092 1.000 N3 0.87090 0.43944 0.73900 1.000 N4 0.61901 0.24365 0.24135 1.000 N5 0.09621 0.40506 0.90654 1.000 N6 0.17501 0.47650 0.65740 1.000 S1 0.01460 0.91539 0.80285 1.000 7-Apr-2000 Hour: 20 Min: 12 Sec: 9 Final RF factor = 9.8725252E-02 Final Rp(F) factor = 9.1044083E-02
Copyright © 1999, 2000 - Armel Le Bail