RMC modelling
F(Q) = [Icoh(Q)-<f2>] / <f>2,
where the <f2> and <f>2 are the usual mean diffusion factors, depending on Q (X-ray) or not (neutron). About 16 million accepted moves were completed before the sixfold constraint was fulfilled, the last of the 300 octahedra was particularly long to be obtained. The whole process took 720 hours CPU on a DEC-ALPHA AXP 4620.
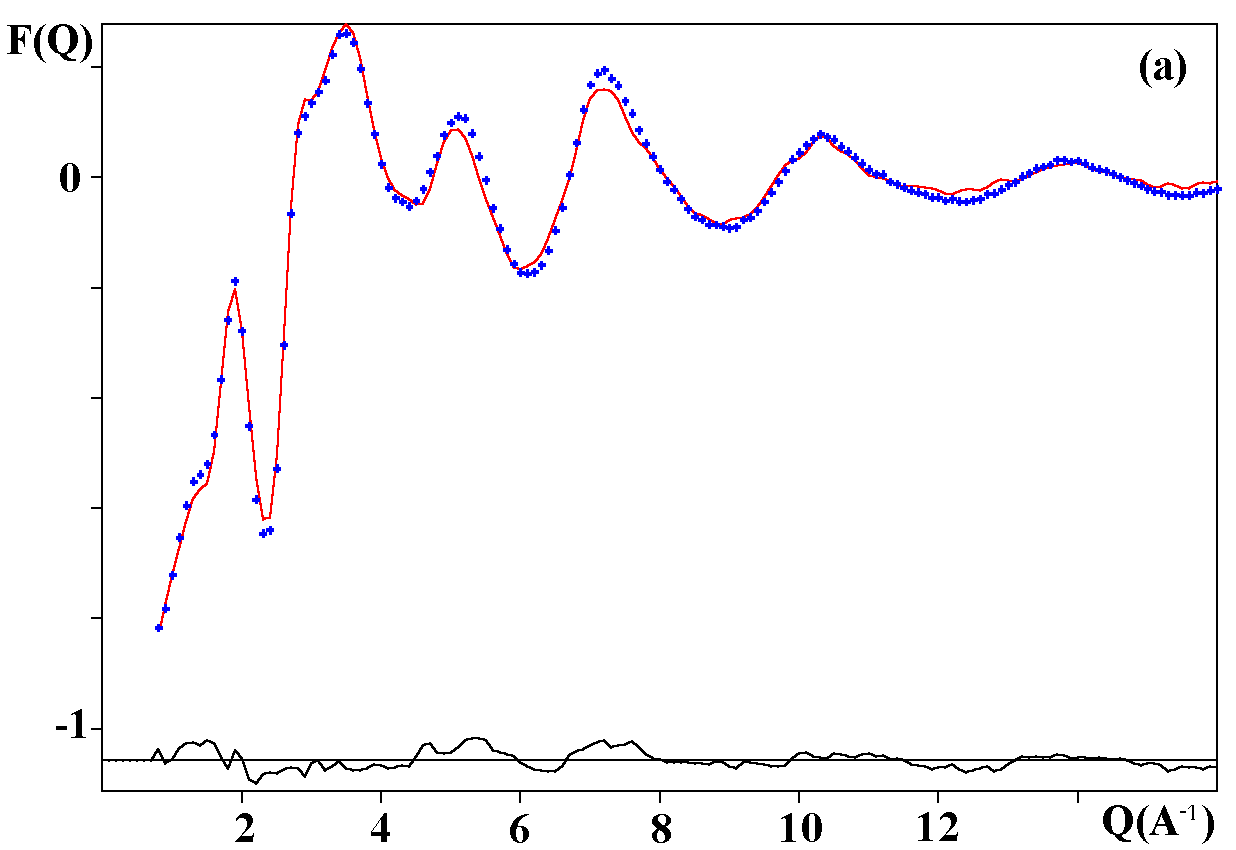
The R factors calculated as 100*|Iobs-kIcalc|/|Iobs| (%) (according to the definition I(Q) = F(Q)+1, k being a scale factor) are 1.42, 1.29 and 1.72 % respectively for the Fe and V-based neutron data and the Fe-based X-ray data. The observed and calculated F(Q) curves are shown on the figure 1. A global view of the octahedra network is shown on the figure 2.
Fig. 1. Experimental (dots) and RMC simulated (solid line) TSF of NaPbM2F9; (a) neutron data for M = Fe, (b) neutron data for M = V, (c) X-ray data for M ) Fe.

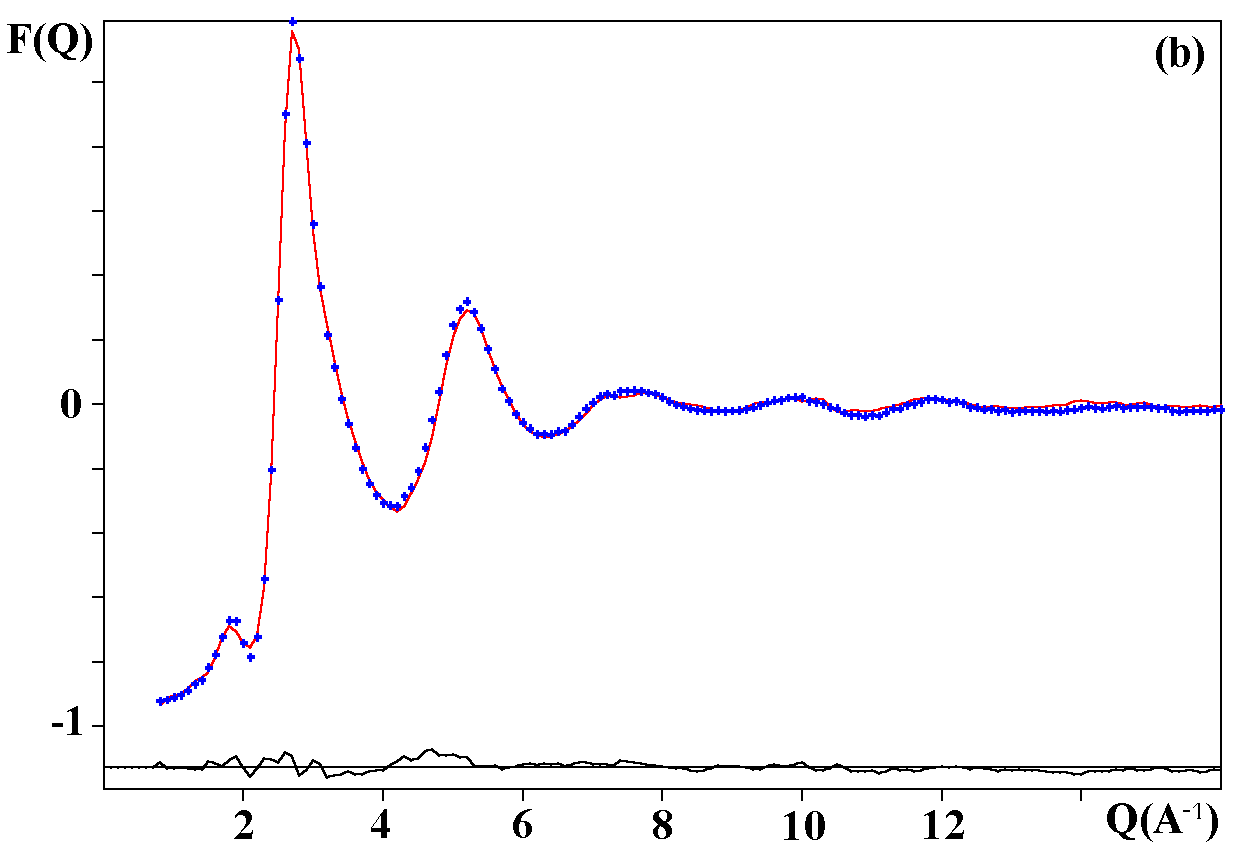
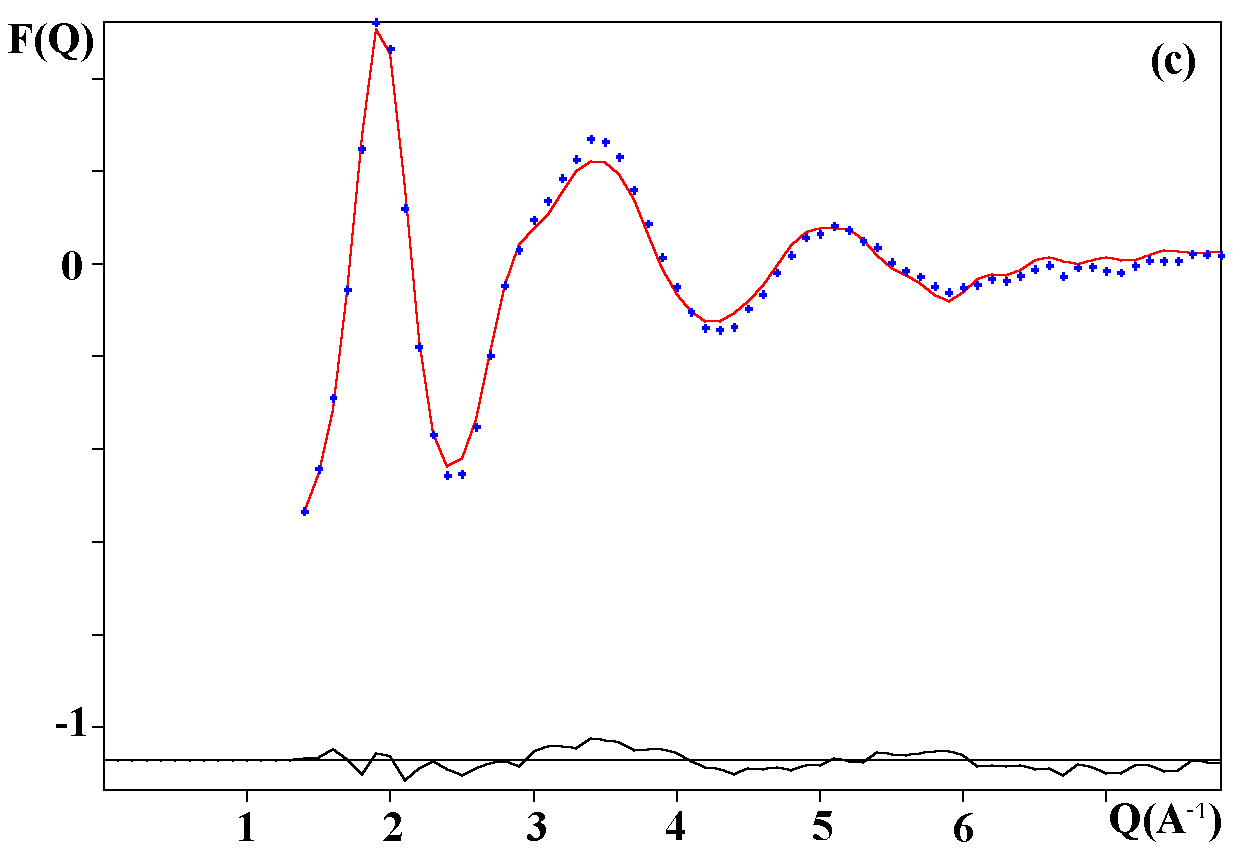
Fig. 2. Projection of the RMC cubic box showing the 300 [MF6] polyhedra network.

-/0/+
Armel Le Bail
- June 1997